Skip to content
Probabilities may be either marginal, joint or conditional. Understanding their differences and how to manipulate among them is key to success in understanding the foundations of statistics.
Marginal probability: the probability of an event occurring (p(A)), it may be thought of as an unconditional probability. It is not conditioned on another event. Example: the probability that a card drawn is red (p(red) = 0.5). Another example: the probability that a card drawn is a 4 (p(four)=1/13).
Joint probability: p(A and B). The probability of event A and event B occurring. It is the probability of the intersection of two or more events. The probability of the intersection of A and B may be written p(A ∩ B). Example: the probability that a card is a four and red =p(four and red) = 2/52=1/26. (There are two red fours in a deck of 52, the 4 of hearts and the 4 of diamonds).
Conditional probability: p(A|B) is the probability of event A occurring, given that event B occurs. Example: given that you drew a red card, what’s the probability that it’s a four (p(four|red))=2/26=1/13. So out of the 26 red cards (given a red card), there are two fours so 2/26=1/13.

How to Manipulate among Joint, Conditional and Marginal Probabilities
The equation below is a means to manipulate among joint, conditional and marginal probabilities. As you can see in the equation, the conditional probability of A given B is equal to the joint probability of A and B divided by the marginal of B. Let’s use our card example to illustrate. We know that the conditional probability of a four, given a red card equals 2/26 or 1/13. This should be equivalent to the joint probability of a red and four (2/52 or 1/26) divided by the marginal P(red) = 1/2. And low and behold, it works! As 1/13 = 1/26 divided by 1/2. For the diagnostic exam, you should be able to manipulate among joint, marginal and conditional probabilities.

———————————
Bayes’ Theorem
Bayes’ theorem: an equation that allows us to manipulate conditional probabilities. For two events, A and B, Bayes’ theorem lets us to go from p(B|A) to p(A|B) if we know the
marginal probabilities of the outcomes of A and the probability of B, given the outcomes of A. Here is the equation for Bayes’ theorem for two events with two possible outcome (A and not A).
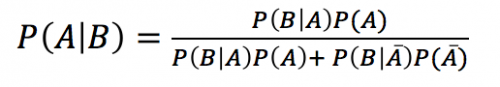
—————————-
Bayes’ Theorem Example
Let’s assume we know that 1% of women over the age of 40 have breast cancer.
[p(cancer)=0.01]
Let’s assume that 90% of women who have breast cancer will test
positive for breast cancer in a mammogram.
[p(positive test|cancer)=0.9]
Eight percent ofwomen that do NOT have cancer will also test positive.
[p(positive test|no cancer)=0.08]
What is the probability that a woman has cancer if she tests positive [p(cancer|positive test)]?
We will call p(cancer) = P(A), and the P(positive test) = P(B). We want to know P(A|B)–the probability of having cancer if you have a positive test.

Using Bayes’ theorem, we calculate that the likelihood that a woman has breast cancer, given a positive test equals approximately 0.10. This makes intuitive sense as (1) this result is greater than 1% (the percent of breast cancer in the general public).
Follow Elizabeth A. Albright, PhD on Twitter @enviro_prof. If you found this page useful, please link or share via Facebook or Twitter. Thanks!
Photo credit: Matthew J. Keedy, Trinidad and Tobago.